曲のテンポ別に
聴く側の感じ方として，
↑遅い
- chord-like
- 和音構成音的
- melody-like
- メロディックなリズムがある
- scale-like or mode-like
- メロディックなリズムが無くアト―ナル
- 高速のボカロ曲とかにある．sheets of sound
↓速い
分類としては全く系統的ではない．
Giant stepsなんかはchord-likeだけどパルスだから上記の枠組みから外れる．
HSP(Hot Soup Processor)で4次元図形を回転させて描画
4次元図形の描画方法として以下のページで述べられていた方法を実装した．
【ゆっくり解説】四次元空間の描き方の基本 - ニコニコ動画
動画「四次元空間の描き方の基本」投稿:本当は怖くない四次元空間 - ブロマガ
以下に作成したプログラムの動作画面を示す．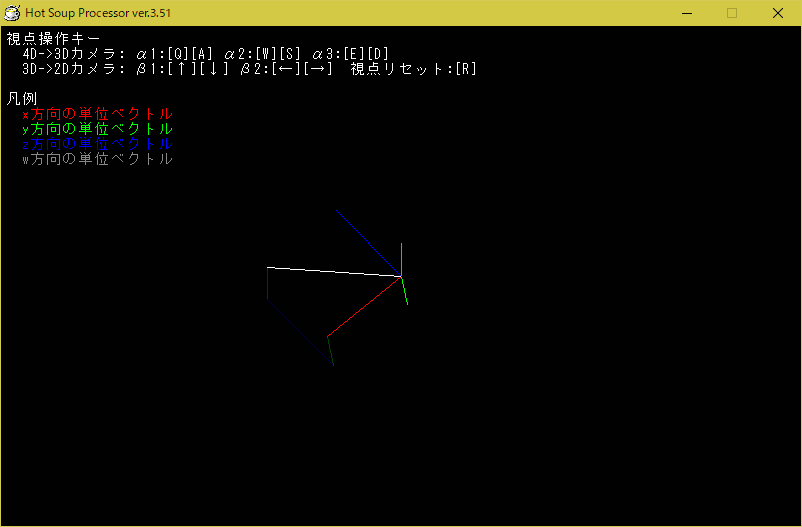
以下のページのコードを改造して本プログラムを作成した．
［HSP］第3回 弾丸の発射 (シューティング・ゲームのミニ講座) - プログラミングのメモ帳(C/C++/HSP)
作成したhspプログラムを以下に示す．
#const eps 0.05 ;角度の増分
*Init
ddim p4,3,4 ;4d->3d行列 縦3 x 横4行列
ddim p3,2,3 ;3d->2d行列 縦2 x 横3行列
; 4d空間カメラ角
a1=0.0:a2=0.0:a3=0.0
; 3d空間カメラ角
b1=0.0:b2=0.0
ddim x4,4 ;4d空間の点座標 縦4 x 横1行列 <- 入力値
ddim x3,3 ;3d空間の点座標 縦3 x 横1行列 <- 中間値
ddim x2,2 ;2d空間の点座標 縦2 x 横1行列 <- 描画時の座標
x4(0)=1.0:x4(1)=1.0:x4(2)=1.0:x4(3)=1.0
wndWidth=800:wndHeight=500 ;ウィンドウサイズ
ddim x0,2 ;描画座標の原点
x0(0)=int(wndWidth/2):x0(1)=int(wndHeight/2)
*Main
screen 0,wndWidth,wndHeight,SCRupz3upz3N_FIXupz3DSIZupz3
font MSGOTHIC,15
gosub *calcDim
repeat
redraw 0
getkey R,82 ;数値リセット R
getkey dnx3,65 ;x下 A
getkey upx3,81 ;x上 Q
getkey dny3,83 ;y下 S
getkey upy3,87 ;y上 W
getkey dnz3,68 ;z下 D
getkey upz3,69 ;z上 E
getkey dnx2,38 ;x下 ↑
getkey upx2,40 ;x上 ↓
getkey dny2,37 ;y下 ←
getkey upy2,39 ;y上 →
if R=1:a1=0.0:a2=0.0:a3=0.0:b1=0.0:b2=0.0:x4(0)=1.0:x4(1)=1.0:x4(2)=1.0:x4(3)=1.0
if dnx3=1:a1-=eps
if upx3=1:a1+=eps
if dny3=1:a2-=eps
if upy3=1:a2+=eps
if dnz3=1:a3-=eps
if upz3=1:a3+=eps
if dnx2=1:b1-=eps
if upx2=1:b1+=eps
if dny2=1:b2-=eps
if upy2=1:b2+=eps
color $01,$01,$01:boxf ;背景
pos 5,5
color $FF,$FF,$FF ;線の色
mes "視点操作キー"
mes " 4D->3Dカメラ: α1:[Q][A] α2:[W][S] α3:[E][D]"
mes " 3D->2Dカメラ: β1:[↑][↓] β2:[←][→] 視点リセット:[R]\n"
mes "凡例"
color $FF,$0,$0 ;線の色
mes " x方向の単位ベクトル"
color $0,$FF,$0 ;線の色
mes " y方向の単位ベクトル"
color $0,$0,$FF ;線の色
mes " z方向の単位ベクトル"
color $88,$88,$88 ;線の色
mes " w方向の単位ベクトル"
;x成分
x4(0)=1.0:x4(1)=0.0:x4(2)=0.0:x4(3)=0.0
gosub *calcDim
px0=x2(0):px1=x2(1)
color $FF,$0,$0 ;線の色
line x0(0),x0(1),x0(0)+int(px0*100),x0(1)+int(px1*100)
px0=x2(0):px1=x2(1)
;y成分
x4(0)=1.0:x4(1)=1.0:x4(2)=0.0:x4(3)=0.0
gosub *calcDim
color $0,$44,$0 ;線の色
line x0(0)+int(px0*100),x0(1)+int(px1*100),x0(0)+int(x2(0)*100),x0(1)+int(x2(1)*100)
px0=x2(0):px1=x2(1)
;原点から
x4(0)=0.0:x4(1)=1.0:x4(2)=0.0:x4(3)=0.0
gosub *calcDim
color $0,$FF,$0 ;線の色
line x0(0),x0(1),x0(0)+int(x2(0)*100),x0(1)+int(x2(1)*100)
;z成分
x4(0)=1.0:x4(1)=1.0:x4(2)=1.0:x4(3)=0.0
gosub *calcDim
color $0,$0,$44 ;線の色
line x0(0)+int(px0*100),x0(1)+int(px1*100),x0(0)+int(x2(0)*100),x0(1)+int(x2(1)*100)
px0=x2(0):px1=x2(1)
;原点から
x4(0)=0.0:x4(1)=0.0:x4(2)=1.0:x4(3)=0.0
gosub *calcDim
color $0,$0,$FF ;線の色
line x0(0),x0(1),x0(0)+int(x2(0)*100),x0(1)+int(x2(1)*100)
;w成分
x4(0)=1.0:x4(1)=1.0:x4(2)=1.0:x4(3)=1.0
gosub *calcDim
color $22,$22,$22 ;線の色
line x0(0)+int(px0*100),x0(1)+int(px1*100),x0(0)+int(x2(0)*100),x0(1)+int(x2(1)*100)
px0=x2(0):px1=x2(1)
;原点から
x4(0)=0.0:x4(1)=0.0:x4(2)=0.0:x4(3)=1.0
gosub *calcDim
color $88,$88,$88 ;線の色
line x0(0),x0(1),x0(0)+int(x2(0)*100),x0(1)+int(x2(1)*100)
;原点からベクトルの総和
x4(0)=1.0:x4(1)=1.0:x4(2)=1.0:x4(3)=1.0
gosub *calcDim
color $FF,$FF,$FF ;線の色
line x0(0),x0(1),x0(0)+int(x2(0)*100),x0(1)+int(x2(1)*100)
px0=x2(0):px1=x2(1)
redraw 1
await (1000/60)
loop
stop
*calcDim
sa1=sin(a1):sa2=sin(a2):sa3=sin(a3):sb1=sin(b1):sb2=sin(b2)
ca1=cos(a1):ca2=cos(a2):ca3=cos(a3):cb1=cos(b1):cb2=cos(b2)
;4d -> 3d行列を定義
p4(0,0)=-sa3
p4(0,1)=ca3
p4(0,2)=0.0
p4(0,3)=0.0
p4(1,0)=-ca3*sa2
p4(1,1)=-sa3*sa2
p4(1,2)=ca2
p4(1,3)=0.0
p4(2,0)=-ca3*ca2*sa1
p4(2,1)=-sa3*ca2*sa1
p4(2,2)=-sa2*sa1
p4(2,3)=ca1
;3d -> 2d行列を定義
p3(0,0)=-sb2
p3(0,1)=cb2
p3(0,2)=0.0
p3(1,0)=-cb2*sb1
p3(1,1)=-sb2*sb1
p3(1,2)=cb1
;4d -> 3dを計算
for j,0,3,1 ;j=0,1,2
temp=0.0
for i,0,4,1 ;i=0,1,2,3
temp+=p4(j,i)*x4(i)
next
x3(j)=temp
next
;3d -> 2dを計算
for j,0,2,1 ;j=0,1
temp=0.0
for i,0,3,1 ;i=0,1,2
temp+=p3(j,i)*x3(i)
next
x2(j)=temp
next
return
Bayesian linear discriminant analysis (BLDA)の論文
Bayesian linear discriminant analysis (BLDA)の論文
https://ieeexplore.ieee.org/document/5166506
https://www.sciencedirect.com/science/article/pii/S0165027007001094
pythonで多次元データの度数分布表を作成（マルチフラクタル次元計算の準備）
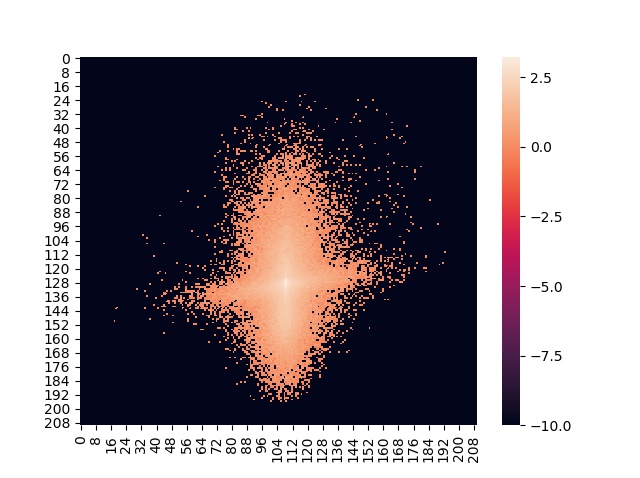
マルチフラクタル次元を計算するため，多次元データの度数分布表を作成するプログラム．
マルチフラクタル次元は，一般化次元（北海道大学の井上 純一先生作成の資料「2009年度 カオス・フラクタル 講義ノート」の第8回や第12回に示される）とも言われる．
以下のプログラムは効率が悪い．
データの特徴量次元を，データ点数を
，ビンの分割数を
とすると，
メモリ空間はに比例し，計算量（ループ回数）は
に比例する．
ソース中のループの実行時間は，約1600秒．ループ一回当たりの実行時間は約0.03秒．
特徴量次元D=2，データ点数N=104847，ビンの分割数V=2 * 3 * 5 * 7とした．
import numpy as np import wave from scipy import fromstring, int16, int64 import itertools import seaborn as sns import matplotlib.pyplot as plt import time def probability_distribution(X, div_num=2 * 3 * 5 * 7): """ 多次元データの度数分布表を作成する． 多次元ヒストグラムあるいは多次元ヒートマップのような，数値の分布を計算する． :param X:入力データ．第0方向が時系列．第1方向が特徴量次元 :param div_num:ヒストグラムで言うところのビンの数 :return: 合計(div_num^D)個の要素を持つ，D次元配列を返す．ここで，Dは特徴量次元数． """ X_max = int64(np.max(X, axis=0)) # 入力データが小数点数ならint64以外にする X_min = int64(np.min(X, axis=0)) # ビン分割の最大値と最小値に余裕を持たせる bin_margin = 0.2 X_max = X_max * (1 + np.sign(X_max) * bin_margin) X_min = X_min * (1 - np.sign(X_min) * bin_margin) bin_resolution = np.array([(X_max - X_min) / div_num]) D = [] # 特徴量次元数 N = [] # データ点数 len_X_shape = X.shape.__len__() if len_X_shape == 2: D = X.shape[1] N = X.shape[0] elif len_X_shape == 1: D = 1 N = X.shape[0] else: return None too_many_D = 30 # 次元が多すぎる場合 if D > too_many_D: import sys print( f"High-dimensional data(data dimension={D}) was input to the function \"{sys._getframe().f_code.co_name}\".\n" f"Do you want to ontinue? [Y]/[N]") if "Y" != input(): print(f"Interrupted was processing of the function \"{sys._getframe().f_code.co_name}.") return None ind_tmp = np.array(list(range(div_num))) ind = np.array(list(itertools.product(ind_tmp, repeat=D))) N_i = np.zeros(np.repeat(div_num, D)) # 度数分布表の配列 start = time.time() # 下のループにかかる時間を測定する． for i in ind: range_min = bin_resolution * i + X_min range_max = bin_resolution * (i + 1) + X_min temp_bin_cond = sum(map(all, np.logical_and(range_min <= X, X < range_max))) N_i[tuple(i)] = temp_bin_cond pass end = time.time() print(f"ループ処理全体に掛かった時間:{(end - start)}") print(f"ループ一周あたりの平均時間:{(end - start) / len(ind)}") sns.heatmap(np.log10(N_i + 1e-10)) # ヒートマップを描画．値の大きさは対数にする． print(f"sum N_i:{np.sum(N_i)} (入力データのデータ数（次元数ではなく）に一致するはず)") return N_i # 度数分布表を返す pass if __name__ == "__main__": file_name = "RIFF wavファイルのパス" with wave.open(file_name, "r") as wf: fs = wf.getframerate() n = wf.getnframes() data = wf.readframes(wf.getnframes()) X = fromstring(data, dtype=int16) # t = np.linspace(0, 10, 1000) # 自分でデータを作る場合 # X = np.sin(2 * np.pi * np.sqrt(101) * t) * 100 # 自分でデータを作る場合 # 特徴量が2次元の時系列データを作成（X[:,0]は時系列データ，X[:,1]は時系列データの時間差分（時間微分）） data = np.concatenate([np.array([X[0:-1]]), np.array([np.diff(X)])], axis=0).T # 上で作成したデータから多次元度数分布表を計算する．ビン分割数は2*3*5*7個としている． probability_distribution(X=data, div_num=2 * 3 * 5 * 7) plt.figure() plt.plot(data[:, 0], data[:, 1]) plt.show() pass
